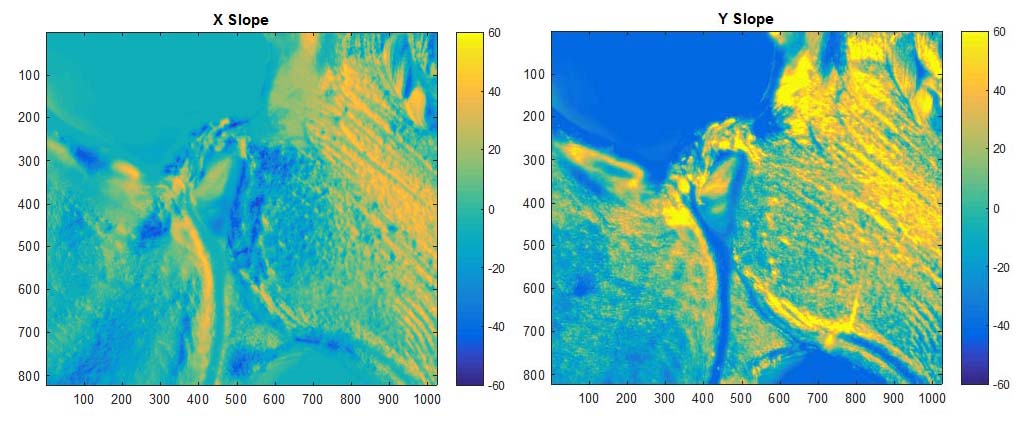
Since the geometry is known in a Disco Lights Illumination system, one can tell a computer which direction each color is coming from. It is fairly straighforward to then assign a value, which I will call the "slope", to each pixel, deriving from the three sector illumination.
The first step is to load, display and crop an input image.

Then, either select RGB as the color channels, or click on three places in the image as representatives of your three colors. Here, I have red, green and yellow filters, so the yellow channel is appropriate (yellow is the inverse of blue, coincidentally). Once the three color channels are known, a vector projection from the known RGB values to the custom channels is done.

With knowledge of the geometry, i.e. that the yellow light is coming from -90°, the red from 30° and the green from 150°, a vector decompostion can be done on the three channels, in x- and y-directions.

We see that the yellow light doesn't contribute to the x-component, as you would expect.
With this information in hand, we can now calculate the x- and y-slopes, averaging the three sector components.
Now that we have the slope maps, integration to determine surface height is done. Here, I use the Inverse FFT method.


And for comparison, here is a stacked image of the same region, but with brightfield illumination.

So far, this image has been the only one that really gave almost reasonable results. Work is continuing on the algorithm, but I will show some of the not-quite-successful attemps, also.
I'm not claiming the heights are correct, or even linear, but this DLI technique seems to show some promise for a single-image technique. Given enough contrast, regular transmitted Rhienberg could also produce 3D data.
The Matlab programs are available here and here (for the integration). No responsibility is taken for their use or misuse!
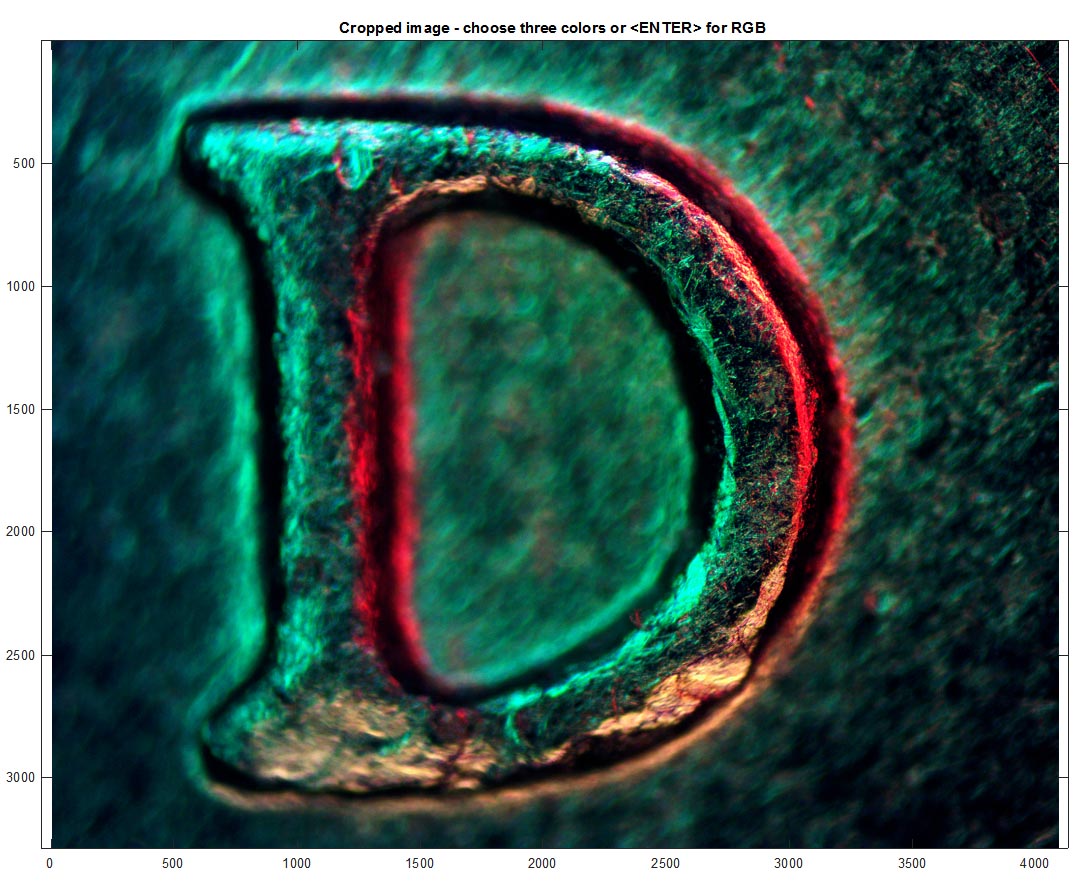
I tried to do the same thing with the image of a "D" for Denver on a U.S. nickel, but found that since the slope was so high, we lost all information there at the "vertical" wall, so the unwrapping to form an image from the "slope" maps failed to create a continuous edge and edge to flat-top transition. It still looks pretty cool in the end, but it is definitely not right.
Following the same steps as before,

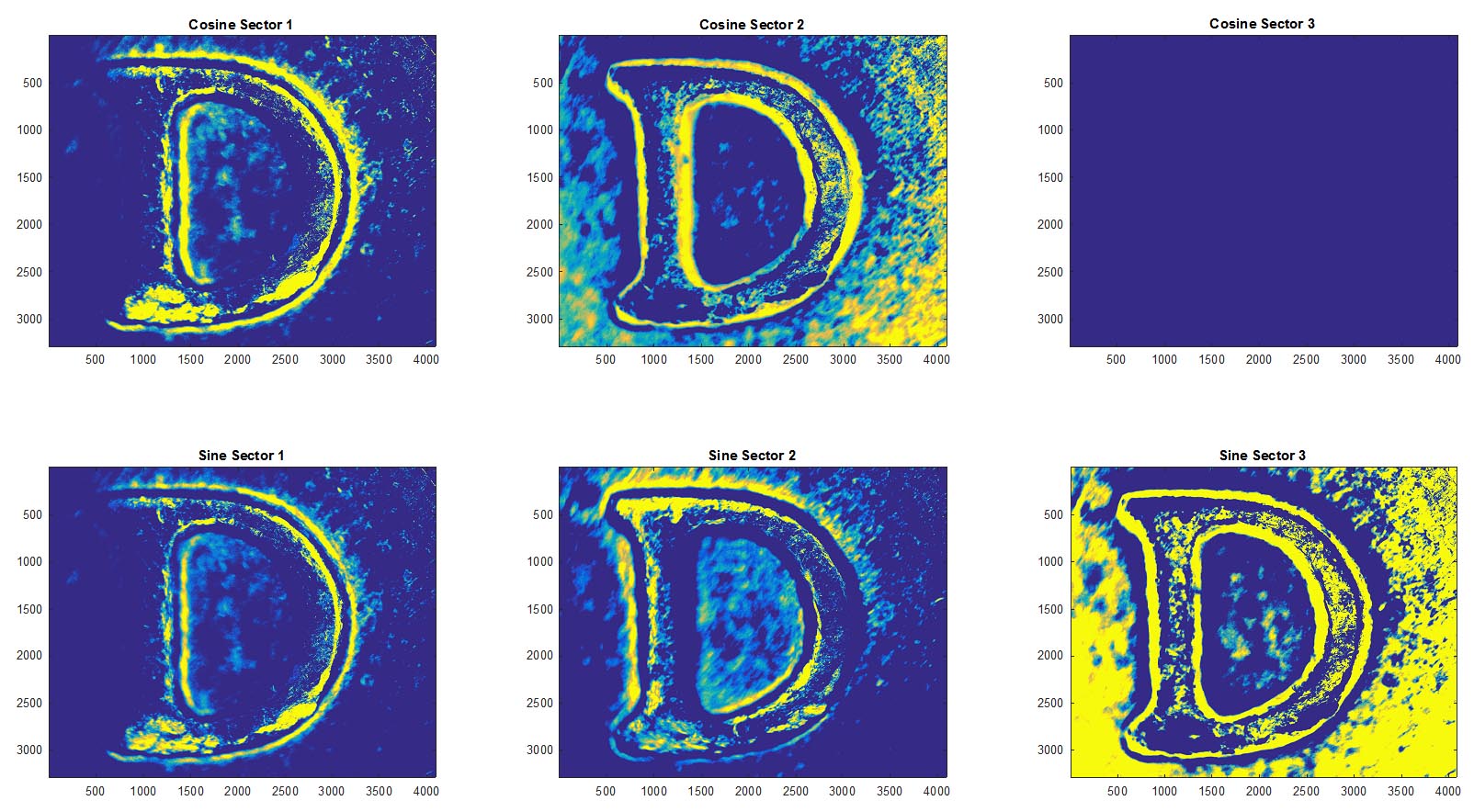

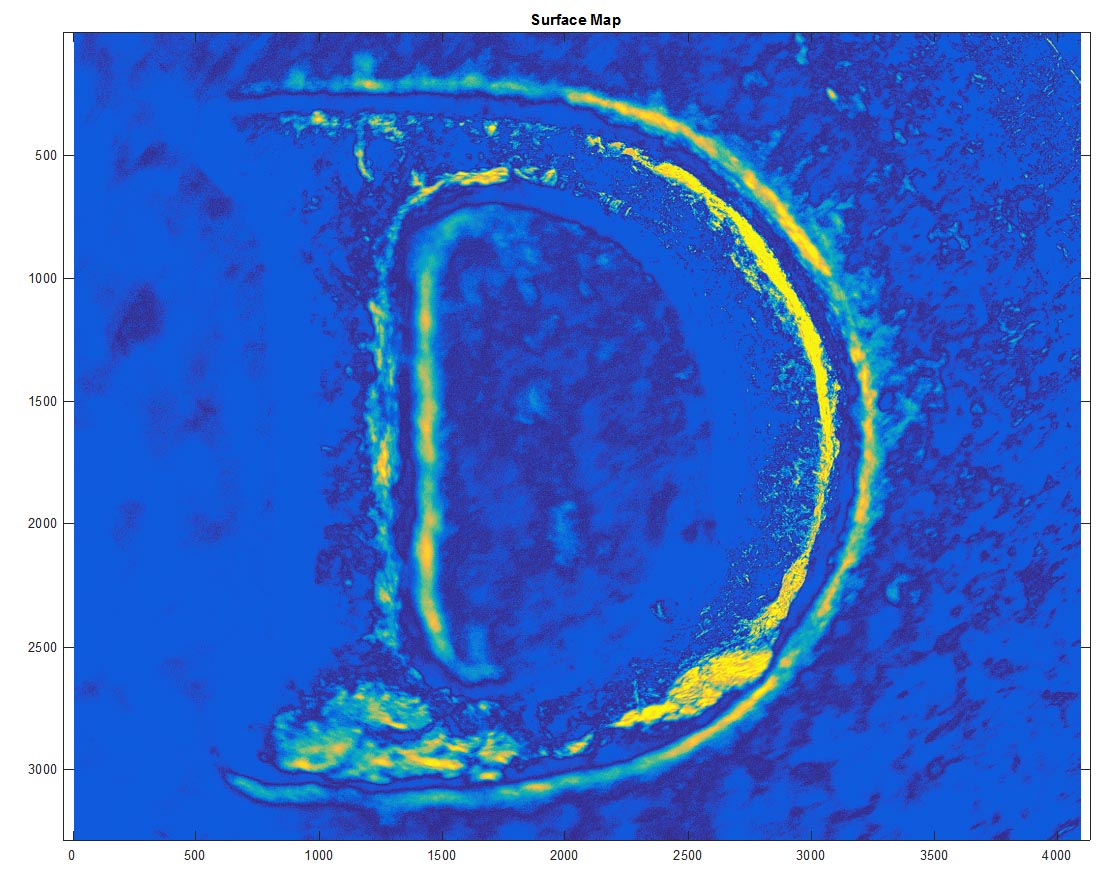


It makes pretty nice "slope" maps, which really are more like edge-finders than accurate slope maps, but it fails to make sense of it in the end.